- Published on
Introduction to Bayesian Optimization
Bayesian Optimization is a powerful and efficient strategy designed to optimize complex, expensive, and noisy objective functions. Proposed in 1978 by J. Mockus, V. Tiešis and A. Žilinskas in the paper “The application of Bayesian methods for seeking the extremum”, this method is widely used in hyperparameter tuning and optimization problems where function evaluations are costly. Bayesian Optimization builds a probabilistic model of the objective function and then exploits this model to select the promising points to evaluate.
Core Concepts
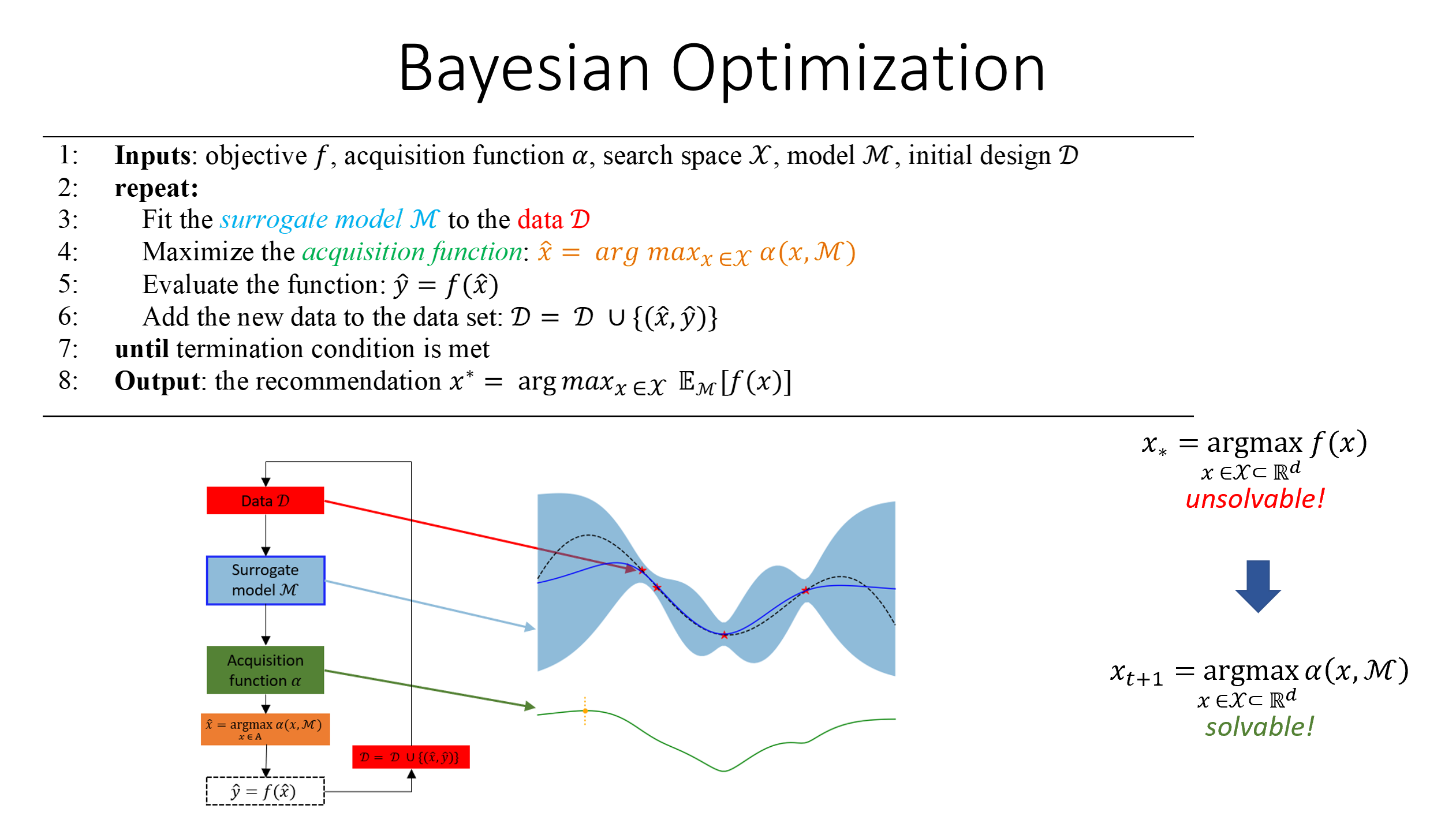
Surrogate Probabilistic Model: Bayesian Optimization utilizes Gaussian Processes (GPs) as the surrogate model, which provides a probability distribution over possible objective functions.
Acquisition Functions: They guide the optimization process by balancing the trade-off between exploring areas of high uncertainty and exploiting areas with low estimated objective values.
How does it work?
- Initialization: Start by evaluating the objective function at some initial points.
- Model Building: Use the function evaluations to build a surrogate probabilistic model (typically a Gaussian Process).
- Choose Next Point: Based on the surrogate model, choose the next point to evaluate the objective function using an acquisition function.
- Iterate: Update the surrogate model based on the new data point and repeat the process.
Why Bayesian Optimization?
- Efficiency: Especially effective when the function evaluations are expensive.
- Noisy Objectives: Can handle noisy objective function evaluations.
- Flexibility: Doesn’t require the objective function to be differentiable.
Common Applications
- Hyperparameter Tuning: Widely used in machine learning to find the best hyperparameters for a model.
- Robotics: For optimizing parameters in control problems.
- Drug Discovery: In finding optimal molecular structures with desired properties.
In Conclusion
Bayesian Optimization provides an intelligent search strategy to navigate through the complex landscape of expensive and noisy functions. By building a probabilistic understanding of the objective function and making guided decisions based on this understanding, Bayesian Optimization often significantly outperforms random or grid search methods, especially in high-dimensional spaces.